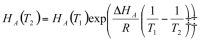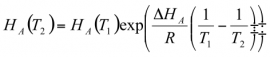Mécanismes

Chimie en phase aqueuse

I Introduction

Les conditions variables de pression et de température à la surface de la terre font coexister l'eau sous les trois formes: gazeuse, liquide, et solide. Les nuages, le brouillard, la pluie, la rosée et les particules d'aérosols liquides sont quelques-unes des différentes formes que peut prendre cette eau. Des réactions en phase aqueuse vont pouvoir donc intervenir dans les différentes formes que peut prendre l'eau liquide dans l'atmosphère. La capacité maximale de vapeur d'eau (saturante) dans l'atmosphère est une fonction de la température, la pression partielle saturante décroissant exponentiellement avec la température. Cette propriété thermodynamique de base de l'atmosphère permet d'expliquer la création de l'eau liquide dans les nuages. Les réactions chimiques dans l'atmosphère dépendront donc de la température à la fois pour leur cinétique propre, et pour la quantité d'eau disponible dans l'atmosphère sous forme nuageuse ou autre.

Loi de Henry

L'équilibre d'une espèce A entre sa phase gazeuse et sa phase liquide peut être représenté par:

 A(g) ↔ A(l) (1)

L'équilibre entre la forme gazeuse de A et la forme dissoute (liquide) est exprimée par la loi de Henry avec le coefficient du même nom HA, selon:

 [A(l)] = HApA eq. 1

Avec: pA est la pression partielle de A dans la phase gazeuse (atm) et [A(l)] est la concentration de A dans la phase liquide (mol l-1 ou M). La constante de Henry HA s'exprime donc mol l-1atm-1 ou M atm-1. Telle qu'exprimée ici, on voit que plus les gaz sont solubles, plus la constante de Henry est forte. La loi de Henry n'est vérifiée que pour les solutions diluées, ce qui est compatible avec les concentrations généralement observées dans l'eau nuageuse. Les valeurs de la constante de Henry intrinsèque, par opposition à la constante effective présentée plus loin, ne rendent compte que de la solubilité physique d'un gaz, et ne tient pas compte, entre autre, du devenir du gaz dans la solution.

La constante de Henry dépend de la température en fonction de l'équation de Van’t Hoff. Si on considère, sur un petit intervalle, que la variation d'enthalpie ΔHA de la réaction ne varie pas, alors l'équation intégrée de Van't Hoff est donnée par:

Ainsi, si on connaît ΔHA à une température donnée, on peut recalculer la constante de Henry à d'autres températures. Comme on peut le constater à partir de l'équation 2, la constante de Henry augmente lorsque T diminue, reflétant ainsi une plus grande solubilité des gaz aux basses températures. Ainsi par exemple pour l'ozone, la constante passe de 9,4 10-3 à 30 10-3 M atm-1 lorsque T passe de 298 à 273K.

Fraction dissoute

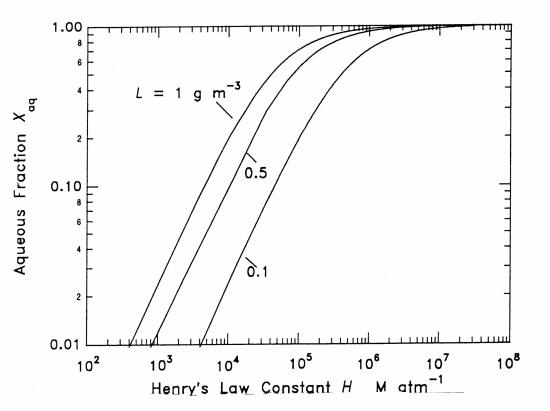
Si l'on compare les solubilités des gaz, un gaz considéré comme soluble dans un contexte peut être considéré comme insoluble dans un autre contexte. Ainsi, l'acétone (HA=25,6 M atm-1) peut être considérée comme soluble si elle est comparée aux hydrocarbures aliphatiques, mais elle est très peu soluble si on la compare au formaldéhyde (HA= 6300 M atm-1). Ainsi, pour comparer les gaz, on s'intéresse plutôt à la fraction de chacun d'entre eux qui est sous forme gazeuse ou liquide dans l’environnement caractéristique d'un nuage moyen. On définit pour cela un facteur de distribution fA pour une espèce A qui se caractérise comme le rapport entre sa concentration en phase liquide cl (g(l air)–1) et sa concentration en phase gazeuse cg (g(l air)–1). Ce facteur est sans dimension car les deux concentrations sont exprimées dans la même unité. Il varie de 0 pour des composés non solubles, à l'infini pour des composés très solubles. A partir de la définition précédente, on peut tracer la fraction de A en phase liquide en fonction de HA (cf. figure 1).

Comme on peut le voir sur la figure 1, les espèces ayant des constantes de Henry inférieures à 400 M atm-1 ont moins de 1% de leur masse dissoute dans l'eau nuageuse. C'est le cas de l'ozone, du NO, du NO2 et des hydrocarbures. A l'opposé, une fraction significative (plus de 10%) se trouve en phase liquide si la constante de Henry est supérieure à 5000 M atm-1 (pour L > 1g m-3). On peut donc classer les espèces en trois catégories:

HA < 1000 M atm-1                 espèces peu solubles

1000 < HA < 10000 M atm-1     espèces modérément solubles

HA > 10000 M atm-1                espèces très solubles

En pratique, et vu les valeurs de la constante de Henry, seules les quatre espèces CH3COOH, H2O2, HNO3 et NO3 peuvent être considérés comme très solubles.

Devenir en solution

Lorsqu'ils se dissolvent dans l'eau, un bon nombre d'espèces se dissocient en ions. Cette dissolution est une réaction réversible qui atteint rapidement son équilibre. L'eau elle-même s'ionise pour former un proton H+ et un ion hydroxyde OH-. On tient compte de cette dissolution en exprimant le produit ionique de l'eau Ke avec:

Ke = [H+][OH-] eq.3

avec Ke = 10-14 M² à T 298K.

Pour de l'eau pure, chaque molécule d'eau dissociée produit un nombre égale de molécules de proton et d'ion hydroxyle. Ainsi, on a:

[H+] = [OH-] = 10-7 M

On rappelle que le pH se calcule à partir de l'équation suivante:

pH = - log10[H+] eq. 4

On a donc un pH égal à 7 pour une eau pure. Il faut noter que la constante de dissociation de l'eau est très faible comparée aux autres constantes d'équilibre. Pour 55,5 molécules d'eau pure, on a seulement une concentration d'ions de 0,2 µM, soit une molécule d'ion pour 300 millions molécules de H2O: on dit que l'eau pure est un électrolyte (de conductivité) très faible.

Acidité naturelle

Le CO2 de l'atmosphère est susceptible de se dissoudre dans l'eau nuageuse (HCO2 = 3.4 10-2 M atm-1). Une fois dissous dans l'eau, le CO2 va se dissocier en deux fois pour donner des carbonates (HCO3-), des bicarbonates (CO32-) et des protons lors de chacune de ces réactions de dissociations:

CO2(g) + H2O ↔ CO2.H2O (2)

CO2.H2O ↔ H+ + HCO3- (3)

HCO3- ↔ H+ + CO32- (4)

La dissolution du CO2 va donc entraîner une acidification de l'eau nuageuse. Compte tenu de la valeur des constantes de dissociation, de la constante de Henry, et en prenant en compte l'électroneutralité du système chimique, on montre que le pH naturel de l'eau nuageuse est aux alentours de 5.6. 

Constante de Henry effective

Le comportement du dioxyde de soufre en solution est comparable à celui du dioxyde de carbone, c'est-à-dire qu'il y a dissolution, puis dissociation en 2 étapes:

SO2(g) + H2O ↔ SO2.H2O (5)

SO2.H2O ↔ H+ + HSO3- (6)

HSO3- ↔ H+ + SO32- (7)

En remarque, on notera que l'écriture SO2.H2O est équivalent à SO2(l), et correspond donc à la partie de SO2 dissoute. On noter a aussi que les différentes formes du soufre présent dans le système (SO2.H2O, HSO3-, et SO32-) est dans le degré d'oxydation* 4 (ou S(IV)).

Les concentrations des espèces dissoutes peuvent être calculées à partir de l'expression de chacune des deux dissociations et de la loi de Henry. On a alors:

[SO2.H2O] = HSO2×pSO2 eq. 5

HSO3- = ks6 [SO2.H2O]/[H+] eq. 6

SO32- = ks7 HSO3- /[H+] eq. 7

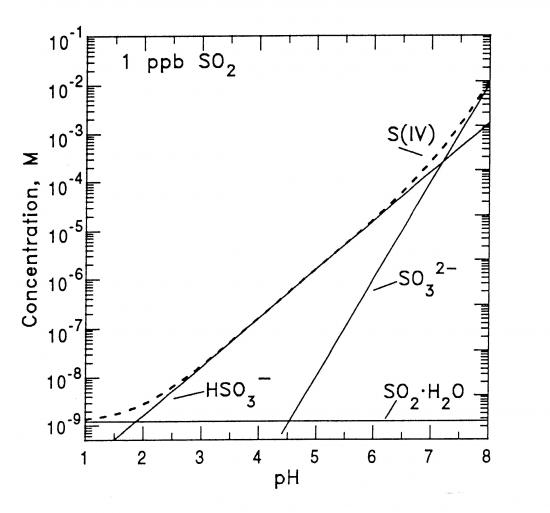
On peut représenter (cf. figure 2) les concentrations du soufre S(IV), en fonction du pH. Comme on peut le constater, lorsque la concentration en H+ diminue, c'est-à-dire lorsque le pH augmente, les concentrations en S(IV) augmentent (sauf pour SO2.H2O qui est indépendant du pH).

Le S(IV) total dissous est égal à:

[S(IV)] = [SO2.H2O] + HSO3- + SO32- eq. 8

⇒ [S(IV)] = HSO2pSO2 x [1+ ks6/[H+] + ks6 ks7/[H+]²] eq. 9

On peut alors définir la constante de Henry effective pour le SO2:

H*S(IV) = HSO2 [1+ ks6/[H+] + ks6 ks7/[H+]²] eq. 10

Le S(IV) total dissous est alors égal à:

=> [S(IV)] = H*S(IV) x pSO2 eq. 11

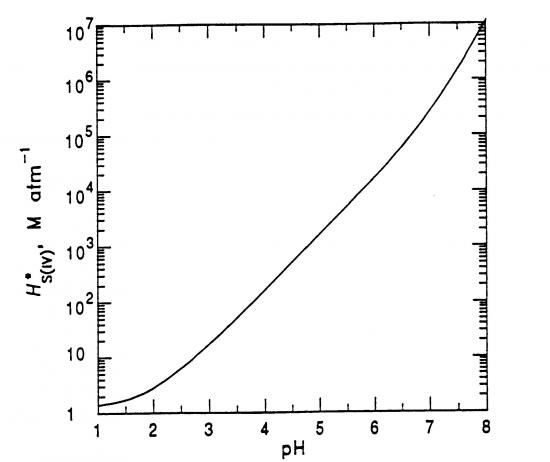
Si l'on compare les valeurs des constantes H*S(IV) et HSO2 (équation 9 et figure 3), on voit que la prise en compte de l'équilibre acide-base augmente la valeur de la constante de Henry, c'est à dire qu’il y a plus SO2 dissous, et cela d'autant plus que le pH augmente. La variation est tout à fait importante puisque le domaine couvert représente sept ordres de grandeur entre la valeur pour un pH de 1 (pas réaliste dans l'atmosphère toutefois) et un pH de 7.

On pourrait aussi représenter les fractions des concentrations du soufre S(IV) dissous en fonction du pH. On monterait que pour un pH inférieur à 2, le S(IV) est principalement sous forme de SO2.H2O, principalement sous forme de HSO3- pour les pH compris entre 3 et 6, et majoritairement sous forme de SO32- pour les pH supérieurs à 7. Les différentes espèces de S(IV) ayant différentes réactivités chimiques, une réaction chimique en solution qui impliquera soit HSO3-, soit SO32-, aura une  vitesse qui dépendra du pH puisque la concentration de ces espèces en solution dépend du pH. Il en va de même pour la plupart des réactions en phase aqueuse qui dépendant pour la plupart du pH du milieu considéré.

Glossaire: 

- Degré d'oxydation: il caractérise l'état électronique d'une espèce chimique (molécule, ion, radical) par rapport à l'état élémentaire neutre servant de référence (degré = 0). Pour les atomes, on a degré nul. Pour les ions monoatomiques, le degré est égal à la charge portée (par exemple +2 pour Mg2+). Degré = -2 pour l'oxygène (excepté pour peroxydes, degré =-1); degré = 1 pour l'hydrogène (composé covalent non métallique); degré = -1 pour le fluor.